The programmable calculator a tool for measurement of extruder performance
Vol. 7 #1, March 1978
In the last few years, the computer industry has made great strides in terms of the reduction of size and cost of solid state computing devices while increasing operating speeds and memory capacity. We now find large scale integration (LSI) being employed in microcomputers for controlling extrusion and injection molding processes as well as in programmable controllers. Another aspect of this technology has been the development of pocket size programmable calculators. This article describes a typical application of a programmable calculator that can be utilized to provide on-line analysis of an operating extruder. The calculations described can be handled on a Texas Instruments SR-52 calculator which has 224 program steps and 22 storage registers.
In extrusion we generally observe motor amperage, screw, RPM, extrudate temperature, throughput rate and pressure developed at the tip of the screw. This analysis utilizes these first four-variables along with information on the screw design, drive motor characteristics and enthalpy of the polymer to gain a better insight into the performance of single stage, single screw extruder. Controlling the feed rate of solids into the extruder is an important aspect of controlling the extrusion process. Some plastics have very sensitive friction characteristics such that conveying efficiency in the feed section of the extruder may range from zero to 40% depending on the temperature of the cylinder in the feed zone. Using the Darnell and Mol (1) theory of solids conveying, the feed efficiency is calculated by:
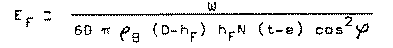 Image 5AS |
Using this equation, we can readily determine the effects of feed zone cylinder temperature, screw cooling in the feed zone, incoming plastic temperature, axial grooves in the inside cylinder surface, etc.
We can gain further insight into the operation of the extruder by comparing the actual throughput to the drag flow rate (the computed flow rate of the metering section of the screw against zero pressure.) Ideally we would observe the drag flow rate if the die and other obstructions to flow were removed and the throughput measured under these conditions. However, due to some randomness in solids feeding it is common practice to overdesign the !d section somewhat. We can compute the fraction of drag flow by: See Bernhardt, (2)
 Image 5BS |
Values of Q NET/Q D generally range from .75 to 1.20. Increasing the pressure will cause Q NET/Q D to decrease along with an increase in extrudate temperature and an improvement in mixing. If the feed section is overdesigned to too great an extent, the feed section forces solids through the extruder at a rate too fast so that melting is completed too late, causing deterioration of extrudate quality. Although it is possible to operate extruders satisfactorily above their theoretical drag flow rate, one should be wary when this ratio exceeds 1.20.
Another useful parameter in extrusion is the mechanical energy input per Unit weight of material. This correlates well with degree of dispersion of a pigment in a polymer and is calculated by:
 Image 5CS |
This equation holds for a DC motor without field weakening. If field weakening is employed or a different type of drive system is used, the appropriate power relationships must be used.
We can compare the mechanical work input with the polymer enthalpy by:
 Image 5DS |
If this ratio is 1.0, we have an adiabatic process on an overall energy balance. Actually, it is common to have heat input in the rear zones and to extract heat in the front zones, so that the process is not truly adiabatic. However, on an overall energy balance we generally find that a single screw extruder performs best when rn/h is about 1.0. If this ratio is greater that 1.0 it means we are extracting heat to maintain the desired extrudate temperature or are purposely providing intensive work to disperse a pigment, for example. If rn/H is much less than 1.0. we frequently observe poor extrudate quality. An exception is hard crystalline polymers which have a high heat of fusion and low melt viscosity, since higher amounts of conducted heat are required to melt these materials.
In practice, the program containing the above equations is placed in the calculator by reading a magnetic card. Next, the values for screw dimension, drive motor power characteristics and polymer enthalpy are entered through the keyboard for storage in the memory registers. During the evaluation run, values of amerpaoe, screw RPM, extrudate temperature and throughput rate are entered and feed efficiency, fraction of drag flow, mechanical work per lb. and mechanical work/enthalpy are computed in a few seconds. The operator can quickly assess the effects of pressure, zone temperature settings, screw speed and screw cooling to determine which of these factors is most effective in terms of achieving the desired results. This approach has been a great help in laboratory evaluation, extruder start-ups, trouble-shooting and developing design data.
LIST OF SYMBOLS
|
LIST OF SYMBOLS |
|
|
|
SYMBOL |
DEFINITION |
UNITS |
|
Cp |
Specific heat of polymer |
BTU/Ib.°F. |
|
D |
Major diameter of screw |
inch |
|
e |
Flight width parallel to axis |
inch |
|
E F |
Conveying efficiency of feed section |
— |
|
E G |
Efficiency of gear reducer |
— |
|
E m |
Efficiency of motor |
— |
|
H |
Enthalpy of polymer |
BTU/lb. |
|
H m |
Enthalpy of melt at melting point of polymer |
BTU/lb. |
|
h F |
Depth of feed section |
inch |
|
h M |
Depth of metering section |
inch |
|
I |
Motor armature current |
amps. |
|
M |
Mechanical work per unit weight |
HP hr./lb. |
|
N |
Screw speed |
RPM |
|
N B |
Base speed of DC motor |
RPM |
|
Q D |
Drag flow rate |
in.3/sec. |
|
Q NET |
Net throughput rate |
in.3/sec. |
|
R G |
Gear reduction ratio |
— |
|
t |
Screw pitch |
inch |
|
T |
Extrudate temperature |
°F. |
|
T rn |
Melting point of polymer |
° F. |
|
V |
Motor armature voltage at base speed |
Volts |
|
W |
Mass throughout rate |
lb./hr. |
|
P B |
Bulk density of feedstock |
lb./in.3 |
|
P M |
Melt density |
lb.Iin.3 |
|
P |
Screw helix angle = arctan |
Deg. |
References:
W.H. Darnell and E.A.J. Mol, SPE Journal, April, 1956.
E.C. Bernhardt, Processing of Thermoplastic Materials, pp 165-228, Reinhold, New York (1965).
— Leonard F. Sansom
See also:
- Extrusion technology - some new findings
- More on the drag flow equation
- Technical developments
Return to
Consultants Corner